默认情况下，Prophet 将返回预测 yhat 的不确定区间。这些不确定区间背后有几个重要的假设。

预测中有三个不确定性来源：趋势中的不确定性、季节性估计中的不确定性以及额外的观测噪声。

趋势中的不确定性

预测中最大的不确定性来源是未来趋势变化的潜力。我们在本文档中已经看到的时间序列显示了历史中明显的趋势变化。 Prophet 能够检测并拟合这些变化，但是我们应该期望未来发生哪些趋势变化呢？我们不可能确定，因此我们做了最合理的事情，我们假设未来将看到与历史相似的趋势变化。特别是，我们假设未来趋势变化的平均频率和幅度将与我们在历史中观察到的相同。我们将这些趋势变化向前投影，并通过计算它们的分布来获得不确定区间。

这种测量不确定性的方式的一个属性是，通过增加 changepoint_prior_scale 来允许更高的速率灵活性，将会增加预测不确定性。这是因为如果我们在历史中建模更多的速率变化，那么我们将会期望未来出现更多的变化，并且使不确定区间成为过度拟合的有用指标。

可以使用参数 interval_width 设置不确定区间的宽度（默认情况下为 80%）。

# R
m <- prophet(df, interval.width = 0.95)
forecast <- predict(m, future)

# Python
forecast = Prophet(interval_width=0.95).fit(df).predict(future)

再次，这些区间假设未来将看到与过去相同的速率变化频率和幅度。这个假设可能不正确，因此您不应该期望在这些不确定区间上获得准确的覆盖率。

季节性中的不确定性

默认情况下，Prophet 只会返回趋势和观测噪声中的不确定性。要获得季节性中的不确定性，您必须进行完整的贝叶斯抽样。这可以使用参数 mcmc.samples（默认为 0）完成。我们在此为快速入门中的 Peyton Manning 数据的前六个月执行此操作

# R
m <- prophet(df, mcmc.samples = 300)
forecast <- predict(m, future)

# Python
m = Prophet(mcmc_samples=300)
forecast = m.fit(df, show_progress=False).predict(future)

这用 MCMC 抽样代替了典型的 MAP 估计，并且根据有多少观测结果，可能需要更长的时间 - 预计需要几分钟而不是几秒钟。如果您进行完整抽样，那么在绘制季节性组件时，您将会看到其中的不确定性

# R
prophet_plot_components(m, forecast)

# Python
fig = m.plot_components(forecast)

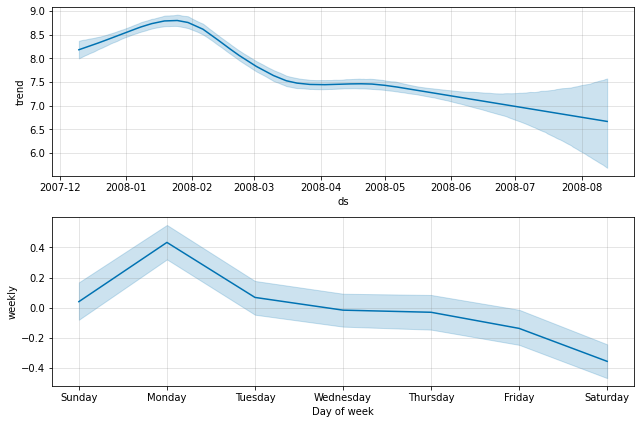
您可以使用方法 m.predictive_samples(future) 在 Python 中访问原始后验预测样本，或者使用函数 predictive_samples(m, future) 在 R 中访问。

在 GitHub 上编辑