诊断
交叉验证
Prophet 包含时间序列交叉验证功能,用于使用历史数据测量预测误差。 这是通过选择历史记录中的截止点,并针对每个截止点,仅使用截止点之前的数据拟合模型来完成的。 然后,我们可以将预测值与实际值进行比较。下图说明了 Peyton Manning 数据集上的模拟历史预测,其中模型拟合到 5 年的初始历史记录,并对一年的范围进行了预测。
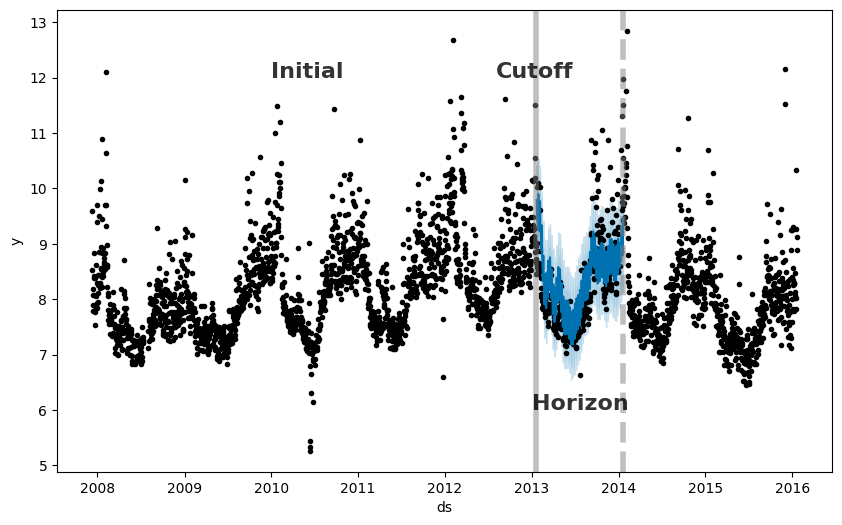
Prophet 论文 进一步描述了模拟历史预测。
可以使用 cross_validation 函数自动针对一系列历史截止点执行此交叉验证过程。 我们指定预测范围 (horizon),然后可以选择指定初始训练期的大小 (initial) 和截止日期之间的间隔 (period)。 默认情况下,初始训练期设置为范围的三倍,并且每半个范围进行一次截止。
cross_validation 的输出是一个数据帧,其中包含每个模拟预测日期和每个截止日期的真实值 y 和样本外预测值 yhat。 特别是,在 cutoff 和 cutoff + horizon 之间的每个观察点都会进行预测。 然后,可以使用此数据帧来计算 yhat 与 y 的误差度量。
在这里,我们进行交叉验证以评估 365 天范围内的预测性能,从第一次截止时的 730 天训练数据开始,然后每 180 天进行一次预测。 在这个 8 年的时间序列中,这对应于总共 11 个预测。
1
2
3
# R
df.cv <- cross_validation(m, initial = 730, period = 180, horizon = 365, units = 'days')
head(df.cv)
1
2
3
# Python
from prophet.diagnostics import cross_validation
df_cv = cross_validation(m, initial='730 days', period='180 days', horizon = '365 days')
1
2
# Python
df_cv.head()
| ds | yhat | yhat_lower | yhat_upper | y | cutoff | |
|---|---|---|---|---|---|---|
| 0 | 2010-02-16 | 8.954582 | 8.462876 | 9.452305 | 8.242493 | 2010-02-15 |
| 1 | 2010-02-17 | 8.720932 | 8.222682 | 9.242788 | 8.008033 | 2010-02-15 |
| 2 | 2010-02-18 | 8.604608 | 8.066920 | 9.144968 | 8.045268 | 2010-02-15 |
| 3 | 2010-02-19 | 8.526379 | 8.029189 | 9.043045 | 7.928766 | 2010-02-15 |
| 4 | 2010-02-20 | 8.268247 | 7.749520 | 8.741847 | 7.745003 | 2010-02-15 |
在 R 中,参数 units 必须是 as.difftime 接受的类型,即几周或更短的时间。 在 Python 中,initial、period 和 horizon 的字符串应采用 Pandas Timedelta 使用的格式,该格式接受几天或更短的时间单位。
也可以将自定义截止点作为日期列表提供给 Python 和 R 中 cross_validation 函数中的 cutoffs 关键字。 例如,三个相隔六个月的截止点需要以如下日期格式传递给 cutoffs 参数
1
2
3
# R
cutoffs <- as.Date(c('2013-02-15', '2013-08-15', '2014-02-15'))
df.cv2 <- cross_validation(m, cutoffs = cutoffs, horizon = 365, units = 'days')
1
2
3
# Python
cutoffs = pd.to_datetime(['2013-02-15', '2013-08-15', '2014-02-15'])
df_cv2 = cross_validation(m, cutoffs=cutoffs, horizon='365 days')
performance_metrics 实用程序可用于计算预测性能的一些有用统计信息(将 yhat、yhat_lower 和 yhat_upper 与 y 进行比较),这是截止点距离的函数(预测在未来有多远)。 计算的统计信息是均方误差 (MSE)、均方根误差 (RMSE)、平均绝对误差 (MAE)、平均绝对百分比误差 (MAPE)、中值绝对百分比误差 (MDAPE) 以及 yhat_lower 和 yhat_upper 估计值的覆盖率。 这些是在按范围排序后,在 df_cv 中的预测滚动窗口上计算的(ds 减去 cutoff)。 默认情况下,每个窗口中将包含 10% 的预测,但可以使用 rolling_window 参数更改此设置。
在 Python 中,您还可以使用 register_performance_metric 装饰器创建自定义性能指标。 创建的指标应包含以下参数
-
df:交叉验证结果数据帧。
-
w:聚合窗口大小。
并返回
- 具有范围和指标列的数据帧。
1
2
3
# R
df.p <- performance_metrics(df.cv)
head(df.p)
1
2
3
4
# Python
from prophet.diagnostics import performance_metrics
df_p = performance_metrics(df_cv)
df_p.head()
| horizon | mse | rmse | mae | mape | mdape | smape | coverage | |
|---|---|---|---|---|---|---|---|---|
| 0 | 37 天 | 0.493358 | 0.702395 | 0.503977 | 0.058376 | 0.049365 | 0.058677 | 0.676565 |
| 1 | 38 天 | 0.499112 | 0.706478 | 0.508946 | 0.058951 | 0.049135 | 0.059312 | 0.675423 |
| 2 | 39 天 | 0.521344 | 0.722042 | 0.515016 | 0.059547 | 0.049225 | 0.060034 | 0.672682 |
| 3 | 40 天 | 0.528651 | 0.727084 | 0.517873 | 0.059852 | 0.049072 | 0.060409 | 0.676336 |
| 4 | 41 天 | 0.536149 | 0.732222 | 0.518843 | 0.059927 | 0.049135 | 0.060548 | 0.681361 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Python
from prophet.diagnostics import register_performance_metric, rolling_mean_by_h
import numpy as np
@register_performance_metric
def mase(df, w):
"""Mean absolute scale error
Parameters
----------
df: Cross-validation results dataframe.
w: Aggregation window size.
Returns
-------
Dataframe with columns horizon and mase.
"""
e = (df['y'] - df['yhat'])
d = np.abs(np.diff(df['y'])).sum()/(df['y'].shape[0]-1)
se = np.abs(e/d)
if w < 0:
return pd.DataFrame({'horizon': df['horizon'], 'mase': se})
return rolling_mean_by_h(
x=se.values, h=df['horizon'].values, w=w, name='mase'
)
df_mase = performance_metrics(df_cv, metrics=['mase'])
df_mase.head()
| horizon | mase | |
|---|---|---|
| 0 | 37 天 | 0.522946 |
| 1 | 38 天 | 0.528102 |
| 2 | 39 天 | 0.534401 |
| 3 | 40 天 | 0.537365 |
| 4 | 41 天 | 0.538372 |
交叉验证性能指标可以使用 plot_cross_validation_metric 可视化,此处显示了 MAPE。 点显示了 df_cv 中每个预测的绝对百分比误差。 蓝线显示了 MAPE,其中平均值是在点的滚动窗口上计算的。 对于此预测,我们看到对于未来一个月的预测,5% 左右的误差是典型的,并且对于一年后的预测,误差会增加到 11% 左右。
1
2
# R
plot_cross_validation_metric(df.cv, metric = 'mape')
1
2
3
# Python
from prophet.plot import plot_cross_validation_metric
fig = plot_cross_validation_metric(df_cv, metric='mape')
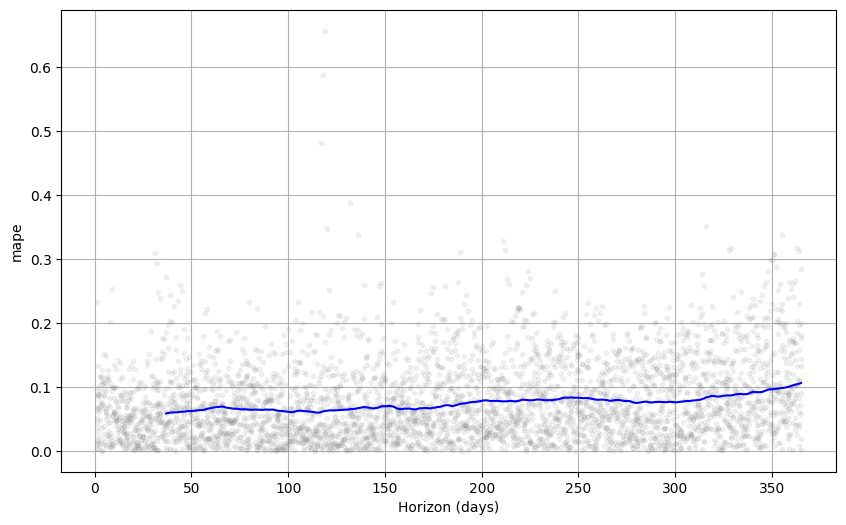
可以使用可选参数 rolling_window 更改图中滚动窗口的大小,该参数指定每个滚动窗口中使用的预测比例。 默认值为 0.1,对应于每个窗口中包含 df_cv 中 10% 的行; 增加此值将导致图中更平滑的平均曲线。 initial 期间应足够长,以捕获模型的所有组成部分,特别是季节性和额外的回归量:年度季节性至少一年,每周季节性至少一周等等。
并行化交叉验证
交叉验证也可以在 Python 中以并行模式运行,方法是设置指定 parallel 关键字。 支持四种模式
-
parallel=None(默认,无并行化) -
parallel="processes" -
parallel="threads" -
parallel="dask"
对于不太大的问题,我们建议使用 parallel="processes"。 当可以在单个机器上完成并行交叉验证时,它将实现最高的性能。 对于大型问题,可以使用 Dask 集群在多台机器上进行交叉验证。 您需要单独安装 Dask,因为它不会与 prophet 一起安装。
1
2
3
4
5
6
7
8
9
10
11
from dask.distributed import Client
client = Client() # connect to the cluster
df_cv = cross_validation(m, initial='730 days', period='180 days', horizon='365 days',
parallel="dask")
超参数调整
交叉验证可用于调整模型的超参数,例如 changepoint_prior_scale 和 seasonality_prior_scale。 下面给出了一个 Python 示例,其中包含这两个参数的 4x4 网格,并在截止点上进行了并行化。 此处参数在 30 天范围内的 RMSE 平均值上进行评估,但不同的性能指标可能适用于不同的问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Python
import itertools
import numpy as np
import pandas as pd
param_grid = {
'changepoint_prior_scale': [0.001, 0.01, 0.1, 0.5],
'seasonality_prior_scale': [0.01, 0.1, 1.0, 10.0],
}
# Generate all combinations of parameters
all_params = [dict(zip(param_grid.keys(), v)) for v in itertools.product(*param_grid.values())]
rmses = [] # Store the RMSEs for each params here
# Use cross validation to evaluate all parameters
for params in all_params:
m = Prophet(**params).fit(df) # Fit model with given params
df_cv = cross_validation(m, cutoffs=cutoffs, horizon='30 days', parallel="processes")
df_p = performance_metrics(df_cv, rolling_window=1)
rmses.append(df_p['rmse'].values[0])
# Find the best parameters
tuning_results = pd.DataFrame(all_params)
tuning_results['rmse'] = rmses
print(tuning_results)
changepoint_prior_scale seasonality_prior_scale rmse 0 0.001 0.01 0.757694 1 0.001 0.10 0.743399 2 0.001 1.00 0.753387 3 0.001 10.00 0.762890 4 0.010 0.01 0.542315 5 0.010 0.10 0.535546 6 0.010 1.00 0.527008 7 0.010 10.00 0.541544 8 0.100 0.01 0.524835 9 0.100 0.10 0.516061 10 0.100 1.00 0.521406 11 0.100 10.00 0.518580 12 0.500 0.01 0.532140 13 0.500 0.10 0.524668 14 0.500 1.00 0.521130 15 0.500 10.00 0.522980
1
2
3
# Python
best_params = all_params[np.argmin(rmses)]
print(best_params)
{‘changepoint_prior_scale’: 0.1, ‘seasonality_prior_scale’: 0.1}
或者,可以通过并行化上面的循环来跨参数组合进行并行化。
Prophet 模型有许多输入参数,可以考虑调整。 以下是一些关于超参数调整的一般建议,这些建议可能是一个好的起点。
可以调整的参数
-
changepoint_prior_scale:这可能是影响最大的参数。 它决定了趋势的灵活性,特别是趋势在趋势变化点处的变化程度。 如本文档中所述,如果它太小,则趋势将欠拟合,并且应该使用趋势变化建模的方差最终将通过噪声项来处理。 如果它太大,则趋势将过度拟合,在最极端的情况下,您最终可能会让趋势捕获年度季节性。 0.05 的默认值适用于许多时间序列,但可以对此进行调整; [0.001, 0.5] 的范围可能大致正确。 像这样的参数(正则化惩罚;这实际上是一种套索惩罚)通常在对数尺度上进行调整。 -
seasonality_prior_scale:此参数控制季节性的灵活性。 同样,较大的值允许季节性拟合较大的波动,较小的值会缩小季节性的幅度。 默认值为 10.,这基本上不应用任何正则化。 这是因为我们很少在这里看到过度拟合(由于它是使用截断的傅里叶级数建模的,因此存在固有的正则化,因此它本质上是低通滤波的)。 调整它的合理范围可能应该是 [0.01, 10]; 当设置为 0.01 时,您应该会发现季节性的幅度被迫变得非常小。 这可能也适用于对数尺度,因为它实际上是一个 L2 惩罚,就像在岭回归中一样。 -
holidays_prior_scale:控制拟合节假日效应的灵活性。类似于 seasonality_prior_scale,默认值为 10.0,基本上不应用任何正则化,因为我们通常有多个节假日的观测值,并且可以很好地估计它们的影响。也可以像 seasonality_prior_scale 一样,将其调整到 [0.01, 10] 范围内。 -
seasonality_mode:选项包括 ['additive','multiplicative']。默认值为'additive',但许多业务时间序列将具有乘法季节性。最好通过查看时间序列,观察季节性波动的大小是否随时间序列的大小而增长来识别(请参阅此处关于乘法季节性的文档),但在不可能的情况下,可以对其进行调整。
也许可以调整?
changepoint_range:这是允许趋势改变的历史比例。默认为 0.8,即历史记录的 80%,这意味着模型不会拟合时间序列最后 20% 中的任何趋势变化。 这是相当保守的,可以避免过度拟合到时间序列末尾的趋势变化,因为没有足够的空间可以很好地拟合它。 通过人工干预,可以很容易地通过视觉识别出来:可以清楚地看到预测在最后 20% 中是否做得不好。 在完全自动化的环境中,减少保守性可能是有益的。使用上述截止点的交叉验证可能无法有效地调整此参数。该模型从时间序列最后 10% 的趋势变化中进行概括的能力很难通过查看早期截止点来学习,这些截止点可能在最后 10% 中没有趋势变化。因此,最好不要调整此参数,除非在大量时间序列中进行调整。 在这种情况下,[0.8,0.95] 可能是一个合理的范围。
可能无法调整的参数
-
growth:选项为“linear”和“logistic”。这可能不会被调整;如果存在已知的饱和点以及朝该点的增长,则将包含它,并将使用逻辑趋势,否则将是线性的。 -
changepoints:用于手动指定更改点的位置。 默认情况下为 None,它会自动放置它们。 -
n_changepoints:这是自动放置的更改点的数量。 默认值 25 应该足以捕获典型时间序列中的趋势变化(至少是 Prophet 可以很好地处理的类型)。 与其增加或减少更改点的数量,不如更有效地关注增加或减少这些趋势变化的灵活性,这可以通过changepoint_prior_scale完成。 -
yearly_seasonality:默认情况下(“auto”),如果有一年的数据,则将打开年度季节性,否则将其关闭。 选项为 [“auto”,True,False]。 如果数据超过一年,而不是尝试在 HPO 期间将其关闭,则更有效地保持其打开状态并通过调整seasonality_prior_scale来降低季节性影响。 -
weekly_seasonality:与yearly_seasonality相同。 -
daily_seasonality:与yearly_seasonality相同。 -
holidays:用于传入指定节假日的数据框。 节假日效应将通过holidays_prior_scale进行调整。 -
mcmc_samples:是否使用 MCMC 可能取决于诸如时间序列的长度和参数不确定性的重要性之类的因素(这些考虑因素在文档中进行了描述)。 -
interval_width:Prophetpredict返回每个组件的不确定性区间,例如预测yhat的yhat_lower和yhat_upper。 这些计算为后验预测分布的分位数,interval_width指定要使用的分位数。 默认值 0.8 提供 80% 的预测区间。 如果需要 95% 的区间,则可以将其更改为 0.95。 这只会影响不确定性区间,而不会改变预测yhat,因此无需进行调整。 -
uncertainty_samples:不确定性区间计算为后验预测区间的分位数,后验预测区间是通过蒙特卡罗采样估计的。 此参数是要使用的样本数(默认为 1000)。 predict 的运行时间将与该数字成线性关系。 使其更小会增加不确定性区间的方差(蒙特卡罗误差),而使其更大将减少该方差。 因此,如果不确定性估计看起来参差不齐,则可以增加它以进一步平滑它们,但可能不需要更改它。 与interval_width一样,此参数仅影响不确定性区间,并且更改它不会以任何方式影响预测yhat; 它不需要调整。